Sobre el calendario persa

junio 22, 2020 admin Deja un comentario

El calendario Iraní, o persa, es solar, con la particularidad de que el año se define por dos pasos aparentes sucesivos del Sol a través del equinoccio vernal (primavera).

Una breve reflexión sobre el calendario Iranio.

M. HEYDARI-MALAYERI – Paris Observatory

61 Avenue de l’Observatoire 75014 Paris,

France. m.heydari@obspm.fr

(traducción del inglés por Gerardo Matallana)

1. Introducción

El calendario Iraní, o persa, es solar, con la particularidad de que el año se define por dos pasos aparentes sucesivos del Sol a través del equinoccio vernal (primavera). Se basa en observaciones astronómicas precisas, y además utiliza un sofisticado sistema de intercalación, que lo hace más preciso que su homólogo europeo más joven, el calendario Gregoriano. Actualmente se usa en Irán como el calendario oficial del país. El calendario Iraní tiene una larga historia multi-milenaria con profundas raíces en la cultura persa, en particular en la herencia Zoroástriaca. Aunque el objetivo de este documento no es el de profundizar en la historia del cálculo del tiempo Iraní dado que las cuestiones abordadas no lo hacen necesario, sí presenta un breve resumen de sus orígenes más remotos. Los lectores interesados pueden encontrar información detallada sobre este tema en, por ejemplo, Taqizâdeh (1938), Birashk (1993), Enciclopedia Iranica y Abdollâhi (1996). La versión actual del calendario es el resultado de una reforma dirigida por el famoso astrónomo, matemático y poeta Omar Khayyâm (1048-1131 de la era cristiana, en adelante AD: Anno Domini) que tuvo lugar en el equinoccio vernal de AD 1079 (viernes, 21 de marzo; ver Nota 1), correspondiente al 1 de Farvardin de AP (Anno Persico) 458. El calendario también se denominó Jalâli, por el nombre del gobernante que ordenó la reforma. En los tiempos modernos, sus principios fueron adoptados oficialmente por el parlamento Iraní el 31 de marzo de 1925 (11 Farvardin AP 1304).

El festival de año nuevo, llamado Nowruz, del persa now “nuevo” + ruz “día”, es también un legado zoroástrico con muchos significados culturales, que simboliza el despertar o el renacimiento de la vida natural después del estéril invierno (Nota 2). Se acompaña, varios días o semanas antes y después del equinoccio de primavera, con ceremonias festivas que conllevan tradiciones centenarias. Podemos, por ejemplo, mencionar la limpieza de la casa y la germinación de semillas antes de la llegada de Nowruz y la fiesta del fuego en la víspera del último miércoles del año, así como el picnic masivo al campo verdeante el día 13 del año nuevo. Hay otras celebraciones, pero su discusión sobrepasa el alcance de este documento. Nowruz ha sido celebrado durante varios milenios por todos los pueblos que viven en Asia Occidental y Central (Afganos, Azeríes, Caucásicos, Kazajos, Kurdos, Kirguises, Tayikos, Turcomanos y otros) independientemente de su origen étnico, religión o idioma. Además de su profundo mensaje, las características no étnicas y no religiosas de Nowruz parecen ser las principales razones por las que ha sido reconocido como patrimonio cultural común por tantos pueblos con antecedentes diferentes.

A pesar de su status sobresaliente, principalmente su precisión y su característica racionalista de basarse en observaciones astronómicas precisas, el calendario Iraní es poco conocido en Occidente. De hecho, pocos estudios han analizado hasta ahora los elementos básicos de su sistema a la luz de los hallazgos astronómicos modernos, aunque algunos trabajos han abordado los orígenes históricos del calendario. En particular, se debe destacar la exactitud del valor de la duración del año en el calendario Iraní, ya que hoy en día existe una confusión generalizada entre los conceptos de año “tropical” moderno y año equinoccio-vernal en el que se basa el calendario Iraní. Una mala interpretación de este tema puede alterar el sistema de intercalación y afectar a la precisión del calendario. Por lo tanto, uno de los objetivos de este documento es aclarar este punto.

El documento no está dirigido solamente a expertos en calendario, sino que se ha hecho un esfuerzo para que también sea accesible a los no especialistas. Está organizado de la siguiente manera. Después de esta Introducción, la Sección 2 presenta una descripción general del calendario Iraní. Luego, en la Sección 3, definimos el año y discutimos su duración utilizando los resultados de investigaciones astronómicas recientes. En la Sección 4 subrayamos la diferencia entre los años “tropical” e Iraní, mientras que el sistema de intercalación, basado en el ciclo de 33 años, queda descrito en la Sección 5. Aunque el documento se centra principalmente en los fundamentos astronómicos del calendario Iraní, no se pasan por alto los aspectos históricos y, en particular, la Sección 6 presenta una breve nota sobre la historia de la reforma liderada por Khayyâm. En los últimos años, algunos expertos en el calendario Iraní han sugerido la presencia de un ciclo de 2.820 años en el calendario Iraní. Discutimos esta cuestión en la Sección 7 y señalamos los defectos de este esquema. La correspondencia entre el Iraní y otros sistemas de calendario se trata en la Sección 8, y la Sección 9 presenta algunos comentarios sobre el antiguo origen del calendario Iraní. Finalmente, en la Sección 10 se recogen las conclusiones finales. A lo largo del documento, se dan explicaciones complementarias en 16 notas que aparecen al final del artículo.

2. Descripción general

Nowruz comienza en el preciso instante en que el Sol, en su curso anual aparente en el cielo, coincide con el equinoccio vernal, un evento que puede ocurrir en cualquier momento durante el período diario de 24 horas. Los equinoccios vernales y otoñales se definen como los puntos de intersección entre la eclíptica (el camino aparente del Sol en el cielo) y el ecuador celeste (la proyección del ecuador de la Tierra en el cielo), aunque el equinoccio vernal es el punto de referencia desde el cual se miden las ascensiones rectas (sistema ecuatorial) y las longitudes (sistema eclíptico) de los cuerpos celestes (Nota 3). El equinoccio vernal también es el momento en que el Sol parece cruzar el ecuador celeste en dirección norte. Sin embargo, hoy en día se define más adecuadamente como el instante en que la longitud eclíptica del Sol es cero grados. El evento Nowruz se mide actualmente con una precisión mejor de 1 milisegundo (Malakpour 2004). Usando las efemérides calculadas por el Institut de Mécanique Céleste et de Calcul des Ephémérides (IMCCE) francés para el intervalo gregoriano AD 1583-2500, encontramos que 584 equinoccios, o aproximadamente el 64% de los eventos completos, ocurren el 20 de marzo para la longitud de Teherán. La distribución entre las fechas cercanas se presenta en la Tabla 1. Cada año, el equinoccio vernal ocurre más tarde, con un retraso generalmente menor de 6 h, con respecto al anterior. El retraso es igual a la fracción del día que excede el año de 365 días completos.

La fecha del equinoccio vernal no sigue a este desplazamiento sistemático hacia adelante porque los retrasos acumulados son absorbidos en el calendario Iraní por el día bisiesto agregado al calendario cada cuatro o cinco años (ver más abajo, Sección 5).

Los datos IMCCE nos han permitido también calcular el desplazamiento dt = t (n + 1) – t (n) para el intervalo +1000 a +2500, siendo t el instante del equinoccio vernal para el año n. Esto da como resultado el valor promedio de 5,81662 h ± 0,00240 (desviación estándar) o 5h 48m 59,83s ± 8s (d.e.), para el intervalo AD 1000-2500. Los límites inferior y superior, 5,54111 y 6,06444 h pertenecen a los años 1095 (AP 474) y 1216 (AP 595), respectivamente. El gráfico que muestra la variación de la demora, dt, a lo largo de los años se muestra en la Figura 1. Dado que la duración del año equinoccio-vernal no es constante (ver más abajo, Sección 3), el desplazamiento promedio depende del intervalo considerado. La Tabla 2 muestra el cambio para varios intervalos diferentes, así como la correspondiente duración del año promedio referida a dos equinoccios vernales sucesivos, en tiempo solar real.

**Tabla 1**. Fechas del equinoccio Iranio Para el período AD 1583-2500
Fecha de Marzo	Frecuencia del evento	Porcentaje (%)
18	0	0
19	33	3,6
20	584	63,6
21	301	32,8
22	0	0

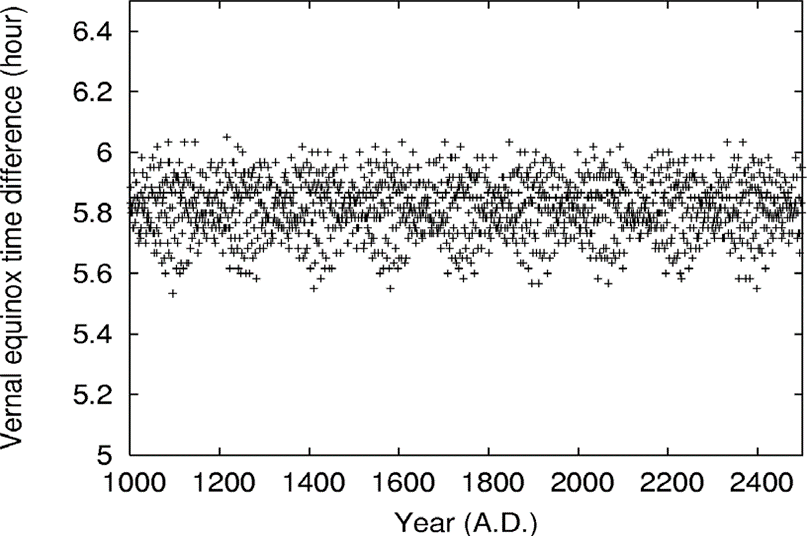
Figura 1. La variación de la demora de tiempo entre un evento de equinoccio vernal con respecto al anterior para el período 1000-2500 AD Valor medio: 5h 48m 59,8s.

Obviamente, el primer día del año del calendario no puede comenzar a la hora exacta del equinoccio vernal y debe comenzar a la medianoche (hora verdadera de Teherán), comienzo del día según una larga tradición Iraní (Nota 4). En consecuencia, si el equinoccio vernal cae antes del mediodía en un día en particular, ese día es el primer día del año. Si el equinoccio vernal ocurre después del mediodía, es el día siguiente cuando comienza el año del calendario. En otras palabras, el año comienza en la medianoche más cercana al instante del equinoccio. En el pasado, esto se lograba observando las altitudes del Sol al mediodía y declarando Nowruz como el día en que la altitud solar excedía por primera vez la altitud del ecuador celeste. Aunque el año del calendario puede comenzar con un retraso o adelanto de menos de 12 h con respecto al evento del equinoccio, el instante exacto del equinoccio vernal, o la transición del año (tahvil-e sâl), tiene la mayor importancia cultural. No importa el momento durante el día o la noche, todos los miembros de la familia, limpios y vestidos con prendas nuevas, esperan el evento astronómico alrededor de una mesa ceremonial (haft-sin) decorada con varios artículos simbólicos. Hoy en día, el instante de Nowruz es transmitido por estaciones de televisión y radio, mientras que en el pasado se usaban disparos de cañón o instrumentos de viento y tambores para señalar el evento. Cuando llega el momento exacto, hay un estallido de alegría y vítores y se intercambian saludos.

**Tabla 2**. Demora de tiempo promedio entre dos equinoccios vernales sucesivos
Intervalo de Época	Desplazamiento (hora) / (h, m, s)	Año promedio (en días solares)
-4000 a +2500	5,81458 5h 48m 52,5s	365,242274
0 a +2500	5,81603 5h 48m 57,7s	365,242335
+1000 a +2500	5,81662 5h 48m 59,8s	365,242359
+1500 a +2500	5,81669 5h 49m 0,1s	365,242362
+1800 a +2200	5,81537 5h 48m 55,3s	365,242307
+800 a +1200	5,81609 5h 48m 57,9s	365,242337
+1995 to +2005	5,83087 5h 49m 51,1s	365,242953

El punto de partida del actual calendario Iraní es el equinoccio vernal ocurrido el viernes 22 de marzo del año 622 AD (Nota 5). Históricamente, el 22 de septiembre de ese año (7º del mes árabe Rabi ‘I), el profeta del Islam emigró a Medina (Hijra). Sin embargo, el segundo califa Umar ibn al-Khatab, cuando adoptó un sistema de calendario alrededor del año 638, prefirió tomar el punto de partida del calendario lunar islámico dos meses y ocho días antes, al comienzo del mes sagrado árabe de Moharram, correspondiente al 19 de julio de AD 622. Por otro lado, el hecho de que en el calendario lunar los meses no están relacionados con las estaciones naturales y las fechas se mueven con respecto al ciclo solar hace que el calendario lunar sea inadecuado para la administración civil (por ejemplo, para la programación agrícola y la recaudación de impuestos sobre la cosecha). Por lo tanto, los problemas introducidos por el calendario lunar repercutieron intensamente en Irán cuatro siglos después durante el reinado de Jalâl ad-Din Malek Shah, de la dinastía Selyucida. Además, la celebración de Nowruz se había deslizado hacia el centro del signo de Piscis, debido a omitir las intercalaciones (ver más abajo, Sección 5), y de hecho, según los primeros historiadores y astrónomos, el objetivo principal de la reforma era fijar Nowruz al equinoccio vernal (Enciclopedia Iranica).

**Tabla 3**. Meses y estaciones Iraníes
Orden	Avéstico (AD c. -2000 a -300)	Persa Medio (AD c. -300 to +700)	Persa Moderno	Días	Estaciones
1	Fravashi/Fravarti [Esencia divina]	Frawardîn	Farvardin	31	Primavera
2	Asha Vahishta [Justicia triunfadora]	Ardawahisht	Ordibehesht	31	Primavera
3	Haurvatât [Totalidad, integridad]	Khordâd	Khordâd	31	Primavera
4	Tishtrya [Sirio, La lluvia de estrellas]	Tîr	Tir	31	Verano
5	Amérétâ [Inmortalidad]	Amurdâd	Mordâd/Amordâd	31	Verano
6	Khshathra Vairya [El buen dominio del elegido]	Shahrewar	Shahrivar	31	Verano
7	Mithra [Sol, amistad, promesa]	Mihr	Mehr	30	Otoño
8	Ap [Agua]	Âbân	Âbân	30	Otoño
9	Âthra [Fuego]	Âdur	Âzar	30	Otoño
10	Dathushô [Creador]	Day	Dey	30	Invierno
11	Vohu Manah [Buena mente]	Wahman	Bahman	30	Invierno
12	Spéntâ Ârmaiti [Santa serenidad]	Spandarmad	Esfand	29/30	Invierno

Por las razones mencionadas anteriormente, el brillante visir y figura política Nezâm-ol-Molk persuadió a Malek Shah para que reformara el calendario. Designó a un grupo de astrónomos encabezados por Omar Khayyâm (Nota 6) que organizaron un observatorio astronómico en la ciudad capital de Isfahan (algunas fuentes han mencionado Rey o Neyshâpur). Sobre la base de observaciones y cálculos, el grupo de expertos adoptó el equinoccio vernal del año 622 AD, que sitúa el comienzo del calendario Iraní seis meses antes de la Hijra. Del mismo modo, inventó un sistema de intercalación único basado en un ciclo de 33 años, que se describe a continuación (Sección 5). Además, el grupo de expertos adoptó 12 meses iguales de 30 días cada uno e insertó los 5 o 6 “días robados” restantes o andargâh (epagomena) entre el 30 de Spandarmad (Esfand) y Nowruz, como se practicaba en el calendario preislámico Iraní. Y, llamativamente, el panel de expertos revivió los antiguos nombres de los meses persas (Tabla 3), aunque se consideraron otras alternativas y se propusieron nuevos nombres poéticos persas.

Notamos, por lo tanto, que el objetivo de la reforma no solo era resolver los problemas administrativos y económicos, sino que también apuntaba a preservar Nowruz, uno de los principales símbolos de la identidad Iraní. En resumen, la reforma tuvo una consecuencia sobresaliente, probablemente sin precedentes en la historia Iraní. Ligó Nowruz firmemente al equinoccio vernal, que no era el caso en el calendario Zoroástrico Sasánida, porque este último aparentemente no empleaba las intercalaciones de 4 años, sino que agregaba un mes suplementario al calendario cada 120 años (de Blois 1996).

A diferencia del calendario islámico, que se basa en el mes sinódico lunar y el correspondiente año lunar de 354 días, el año Iraní se divide en 12 meses con vínculos estrechos con las estaciones anuales reales. Los primeros 6 meses del calendario moderno tienen 31 días, los siguientes 5 meses 30 días y el último 29 o 30 días. Este esquema de duración de los meses está de acuerdo con el hecho de que las estaciones astronómicas no tienen el mismo número de días, siendo la primavera y el verano más largos que el otoño y el invierno (Nota 7). Los nombres de los meses, en su forma Avéstica original (Nota 8), sus significados y su evolución lingüística a lo largo de los siglos se presentan en la Tabla 3.

3. La duración del año.

El año Iraní es un “año tropical” con el equinoccio vernal como punto de referencia. Sin embargo, no debe confundirse con el año tropical establecido por los astrónomos modernos (Nota 9).

Hoy en día, el año tropical se define como el intervalo durante el cual la longitud media del Sol, referida al equinoccio medio de la fecha, aumenta en 360 grados. Esta definición fue adoptada por la Unión Astronómica Internacional en su Asamblea General en Dublín en septiembre de 1955 (Seidelmann et al. 1992). Varios investigadores, en particular Meeus y Savoie (1992), Cassidy (1996) y Meeus (2002) han subrayado la diferencia entre el año equinoccio-vernal y el año tropical recién introducido. Sin embargo, por desgracia se ha difundido en gran medida el error de considerar iguales a ambos. De hecho, la mayoría de los astrónomos y adeptos al calendario están definiendo para sus cálculos el año tropical como comenzando con el equinoccio vernal pero usando la duración del año tropical recientemente definido (Nota 10). Y desafortunadamente, algunos astrónomos Iraníes y expertos en calendarios no están exentos de esta confusión.

Cabe destacar que este nuevo concepto del año tropical, introducido para los estudios de la mecánica celeste, se basa en la longitud media del Sol y no depende de un origen específico para el movimiento anual aparente del Sol. Apunta al comportamiento del año a largo plazo teniendo en cuenta la precesión (en términos de siglos) y no las perturbaciones gravitacionales periódicas de plazo corto. Sin importar cuán útil sea este concepto, los calendarios solares tradicionales, tanto Iraníes como Gregorianos (Nota 11), se basan en la duración media del año equinoccio-vernal real. El propio uso de la nomenclatura tal como ahora está se presta a confusión, porque se usa el mismo término (año tropical) para dos conceptos diferentes, pero muy relacionados. Por lo tanto, sería muy conveniente que la Unión Astronómica Internacional eliminase la ambigüedad adoptando dos términos distintos para ambas nociones. Sería bastante lógico aplicar “año tropical” solo en su significado mecánico celeste moderno, y usar el término “año equinoccio-vernal” para el intervalo entre dos pasos sucesivos del Sol a través del equinoccio vernal. Naturalmente, los Iraníes lo llaman el año Nowruz.

Veamos más de cerca la diferencia entre los años tropical y equinoccio-vernal. Bretagnon y Rocher (2001) dan la siguiente expresión para la duración del año tropical:

365,24219052 – 61,56 10^-6 T – 68,4 10^-9 T² + 263,0 10^-9 T³ + 3,2 10^-9 T⁴[1]

donde T es el tiempo dinámico baricéntrico (TDB) o, más sencillamente, días uniformes (efemérides) de 86.400 segundos (Tiempo Atómico Internacional, TAI), contados en milenios Julianos (de 365,250 días) desde la época actual. La expresión es válida durante un intervalo de ± 10.000 años desde J2000.0. Expresados en tiempo universal, basados en la rotación de la Tierra alrededor de su eje, los mismos autores dan la siguiente fórmula polinómica para el año tropical:

365,2421789 – 135,63 10^-6 T – 68,4 10^-9 T² + 263,0 10^-9 T³ + 3,2 10^-9 T⁴[2]

donde T aquí es el tiempo universal. Por lo tanto, vemos que en la época de J2000 la duración del año tropical era 365,24219052 días uniformes de 86.400 segundos, que es igual a 365,2421789 días solares reales, y se puede redondear a 365,2422 días. Las fórmulas [1] y [2] también indican que la duración del año tropical no es constante. Como se muestra también en la Figura 2, está disminuyendo en aproximadamente 5 milisegundos por año, porque la precesión se está acelerando actualmente. Además, no se muestra en la Figura 2, su longitud en días solares reales disminuye aproximadamente otros 6 milisegundos por año como resultado de la desaceleración de la rotación de la Tierra sobre su propio eje, principalmente debido al efecto de marea de la Luna. Debe subrayarse que actualmente no podemos predecir con precisión la duración del día. La razón es que la rotación de la Tierra sufre variaciones impredecibles e irregulares en diferentes escalas de tiempo, como resultado de procesos geofísicos internos y externos y perturbaciones astronómicas.

Por otro lado, el intervalo de tiempo medio entre dos equinoccios vernales sucesivos, según lo derivado por Meeus (2002) para la verdadera longitud del Sol, basado en los elementos orbitales de la Tierra (Simon et al. 1994) y la solución exacta de La ecuación de Kepler, está representada por la expresión polinómica:

365,2423748 + 10,34 10^-5 T – 12,43 10^-6 T² – 22,63 10^-7 T³ + 1,1 10^-7 T⁴ [3]

para el período comprendido entre aproximadamente 500 B.C. hasta 4500 AD, donde T se mide en milenios julianos de 365,250 (efemérides) días uniformes desde la época J2000.0. Se debe subrayar que esta expresión representa la evolución global del año equinoccio-vernal real para grandes períodos de tiempo al considerar el movimiento Kepleriano no uniforme de la Tierra. Sin embargo, no tiene en cuenta las fluctuaciones en la duración del año causadas por diversas perturbaciones gravitacionales periódicas. La solución exacta se obtiene en las efemérides de IMCCE mediante una ecuación compuesta de 96 términos. La ecuación anterior [3] se puede expresar en días solares, como:

365,2423632 + 2,93 10^-5 T – 12,43 10^-6 T² – 22,63 10 ^-7 T³ + 1,31 10^-7 T⁴ [4]

La comparación entre las ecuaciones [3] y [1] o [4] y [2] muestra claramente que la media de los años equinoccio-vernales y los tropicales no tiene la misma duración. Por ejemplo, para la época de +2000, el año tropical promedio es de 365,2421789 días, mientras que el año medio equinoccio-vernal es de 365,242362 días, es decir, 15,82 s. más. De la misma manera que el año tropical se redondeó a 365,2422 días, el año equinoccio-vernal se puede aproximar a 365,2424 días. Además, es obvio por la ecuación [3] que el año del equinoccio-vernal varía con las edades (ver también la Figura 2). Alrededor de la época -3000 eran 365,241872 días uniformes, mientras que y al comienzo de la era cristiana aumentaba a 365,242138 días uniformes. Todavía está aumentando y alcanzará su mayor valor, 365,242525 días uniformes, en la época +5000. Por lo tanto, la diferencia entre el año equinoccio-vernal y el año tropical no se limita solo a su duración, ya que sus variaciones a largo plazo a lo largo del tiempo también son diferentes. En contraste con el año equinoccio-vernal, el año tropical disminuirá continuamente al menos hasta la época +8000.

La Figura 2 también muestra la variación del año equinoccio-vernal real, en días solares, obtenido por los cálculos de IMCCE. Esos datos se muestran en dos formas diferentes en aras de una mejor visibilidad, ya que el año exhibe fluctuaciones considerables en períodos relativamente cortos. Los puntos discretos, centrados en barras verticales, representan un valor medio para un intervalo de 500 años con las barras que muestran la desviación estándar durante ese intervalo. El rango más pequeño de las fluctuaciones pertenece a la época 0, donde el equinoccio vernal varía durante unos 20 segundos, mientras que para la época +2000 la extensión es dos veces mayor. La curva ondulada muestra los datos IMCCE después de ser suavizados por un método de filtrado en el que se eliminan todas las variaciones con períodos inferiores a 100 años. Por lo tanto, vemos que las principales fluctuaciones en la duración del año equinoccio-vernal son el resultado de perturbaciones de períodos relativamente cortos. La forma general del año equinoccio-vernal real se aproxima a la del año medio equinoccio-vernal si utilizamos una técnica de suavizado más fuerte. Téngase en cuenta que para convertir los días uniformes en días solares, debe usarse un parámetro de corrección, llamado derivada de Delta-T, que puede representarse por la diferencia entre las ecuaciones [1] y [2]. En general, la corrección aumenta los años de día uniforme antes de la época +2000.0 y los reduce después de esa época (Nota 12).

Como se señaló anteriormente, la duración del año equinoccio-vernal real puede desviarse considerablemente del valor medio en períodos cortos, principalmente debido a la atracción gravitacional de la Luna y los planetas. Las fluctuaciones de la duración del año también son visibles en la Figura 1. Durante el intervalo 1000-2500 AD, el año más corto, 365,230880 días, es 1095 AD y el más largo el año 1216 AD con 365,252685 días, o 365d 6h 3m 52,0s. La duración media depende del intervalo considerado, como se muestra en la Tabla 2. Vemos que alrededor de la época de Khayyâm la duración media del año equinoccio-vernal durante el intervalo de 400 años AD 800-1200 fue 365,242337 días solares, que también es el valor promedio para todo el período de 0 a +2500. De este punto en adelante usaremos un valor medio de 365,242362 días (correspondiente al período +1500 a +2500) para la duración del año equinoccio-vernal en los próximos siglos.

Figura 2. Las duraciones de los años tropicales y equinoccio-vernales varían según las edades, mostradas con curvas llenas y punteadas respectivamente, ambas en unidades de días uniformes (efemérides). La duración del año equinoccio-vernal real, en días solares, o el año Iraní, obtenido por las efemérides de IMCCE, se muestra de dos maneras. Los puntos discretos representan valores medios en intervalos de 500 años con sus correspondientes desviaciones estándar mostradas por las barras verticales. Del mismo modo, la curva ondulada muestra una versión suavizada de los datos de efemérides en la que se eliminan las fluctuaciones con períodos menores de 100 años. Las líneas horizontales muestran las duraciones de los años del calendario de Khayyâm y Gregoriano. Están destinadas para comparar con la duración de los años equinoccio-vernales en días solares representados por los datos del IMCCE.

4. La diferencia entre los años “tropical” e Iraní

Aquí damos más explicaciones para resaltar el hecho de que el año Iraní equinoccio-vernal no es igual al recientemente introducido “año tropical”. Dado que la órbita de la Tierra alrededor del Sol es elíptica, su velocidad orbital no es uniforme. En el perihelio de su órbita, es cuando la Tierra está más cercana al Sol y, por lo tanto, se mueve más rápido que el promedio, mientras que en el afelio, cuando está más alejado del Sol, se mueve más lentamente. Además, debido a la precesión, el equinoccio vernal retrocede lentamente a lo largo de la eclíptica en 50,3 segundos de arco por año con respecto a las estrellas, mientras que el eje principal de la órbita de la Tierra gira en sentido directo en 11,6 segundos de arco por año. En consecuencia, cuando el Sol cruza el punto del equinoccio vernal, tardando un año en su camino aparente a lo largo de la eclíptica, la Tierra no ha realizado aún un circuito completo. Ha realizado un viaje completo en una órbita distorsionada (debido a la rotación de la órbita) menos un pequeño arco. Este pequeño arco está cubierto con una velocidad algo diferente, de acuerdo con su posición con respecto al perihelio de la órbita de la Tierra. Como resultado, dependiendo del punto de partida adoptado para el “año”, el circuito completo en longitud tropical tendrá una duración con alguna variación. Esto significa que la duración de un año tropical “real” depende del punto de referencia elegido en la eclíptica.

Una simple fórmula matemática puede facilitar la explicación. La duración del año puede representarse por: Y = T – t, donde T es el tiempo que necesita el Sol para hacer un circuito completo con respecto al perihelio y t el tiempo ganado porque el punto de referencia se acerca al Sol. El tiempo ganado está representado por la relación de la longitud del arco, S, y la velocidad aparente del Sol: t = S / V. Pero como la longitud del arco es constante, t depende solo de la velocidad. Por ejemplo, en el solsticio de diciembre, la Tierra está cerca del perihelio (al que llega a principios de enero) y el Sol aparentemente se mueve más rápido que el promedio hacia el punto de solsticio. Por lo tanto, el tiempo ganado es menor que el del equinoccio vernal, y el año tropical medido para este punto no solo será más largo que el del equinoccio vernal, sino el más largo de los cuatro años cardinales. Sobre la base de las efemérides planetarias calculadas por Simon et al. (1994), Meeus (2002) ha calculado los intervalos medios entre dos pasos sucesivos del Sol a través de los cuatro puntos estacionales durante varias épocas. Los resultados, enumerados en la Tabla 4, muestran claramente que estos diversos años “tropicales” no tienen la misma duración (Nota 13). Y, más particularmente, el año equinoccio-vernal es diferente del año “tropical”. De hecho, el año “tropical” representa el valor medio de las cuatro cifras estacionales (Nota 14). Se debe enfatizar que las duraciones de los años que figuran en la Tabla 4 están en días uniformes, y deben convertirse en días solares para el uso del calendario, como se indica en la segunda fila para el año equinoccio-vernal (Nota 12).

Tabla 4. Diversos años “tropicales” para varias épocas *

Época

Año Nowruz

equinoccio-vernal

Año solsticio-

vernal

Año equinocio-otoñal

Año solsticio-

invernal

-1000

365,242022
365,24223

365,241859

365,242718

365,242871

365,242138
365,24227

365,241726

365,242496

365,242883

+1000

365,242261
365,24232

365,241648

365,242257

365,242840

+2000

365,242375
365,24236

365,241627

365,242018

365,242741

+3000

365,242464
365,24237

365,241659

365,241800

365,242594

+4000

365,242516
365,24235

365,241734

365,241620

365,242407

* Las duraciones de los años están en días de efemérides (uniformes), excepto el año equinoccio-vernal que también se da en días solares reales.

La duración del año en el calendario Iraní, según lo concebido por Khayyâm et al., Es 365,2424… días (Youschkevitch & Rosenfeld 1973), una consecuencia lógica del sistema de intercalación: 365 + 8/33 = 365,2424… (ver Sección 5) Esto está de acuerdo con la duración del año en su tiempo, 365,2423 días. La estimación de Khayyâm de la duración del año coincide aún mejor con el valor medio actual de 365,2424 días. En comparación con el año gregoriano de 365 + 1/4 – 1/100 + 1/400 = 365 + 97/400 = 365,2425 días, el valor de Khayyâm se basó en un conocimiento más preciso del movimiento solar anual. Téngase presente que recientemente se ha atribuido a Khayyâm (O’Connor y Robertson 1999) un valor extremadamente preciso para la duración del año (365,24219858156 días), aunque, por lo que sabemos, no está basado en ninguna fuente histórica. Creemos que este puede ser un valor espurio resultante del ciclo erróneo de 2.820 años sugerido recientemente (ver más abajo la Sección 7).

El conocimiento preciso de la duración del año es una cosa, usarlo prácticamente para construir un sistema de calendario es otra, porque el año de calendario de 365 días enteros no es igual al año solar real. Por lo tanto, un buen calendario es aquel cuyo sistema de intercalación produce un año de duración lo más cercano posible a la realidad.

5. El sistema de intercalación

El desplazamiento promedio del tiempo, dt, entre dos equinoccios vernales sucesivos, listado en la Tabla 2, indica también el exceso de tiempo con respecto al año calendario de 365 días completos. En otras palabras, cada año el tiempo solar adelanta en dt/24 días con respecto al calendario. Tomando dt = 5,81662 h. para el intervalo +1000 a +2500, este adelanto será 5,81662/24 = 0,242359 0,2424 días por año. Por lo tanto, después de cuatro años, el adelanto asciende a 4 x 0,24236 = 0,96944 días, que es aproximadamente 1 día, lo que requiere un año bisiesto de 366 días. Sin embargo, esta corrección de 1 día cada 4 años es demasiado generosa y, por lo tanto, da como resultado un adelanto del año calendario sobre el año solar. Este punto constituye el problema fundamental de los calendarios solares, y esta es la razón por la cual en el calendario Iraní la intercalación no se lleva a cabo sistemáticamente cada 4 años (ver más abajo). Por otro lado, si no se aplican intercalaciones, la fiesta de Nowruz retrocederá con respecto al equinoccio vernal, moviéndose a través de todas las estaciones en aproximadamente 1.506 años. Más explícitamente, después de cuatro años, el equinoccio vernal tendrá lugar en Farvardin 2 y después de ocho años en Farvardin 3, y así sucesivamente. Al mismo tiempo, Nowruz se deslizará más y más hacia el invierno.

El calendario Iraní tiene un ciclo básico de intercalación de 33 años, que consiste en 33 x 0,2424 = 7,9992 = 8 años bisiestos de 366 días y 25 años ordinarios de 365 días. Hay dos tipos de años bisiestos: i) año bisiesto después de 3 años ordinarios (llamado cuadrienal), y ii) año bisiesto después de 4 años ordinarios (quinquenal). Durante un período cuadrienal, el equinoccio vernal ocurre sistemáticamente como dos pares: dos veces después del mediodía y luego dos veces antes del mediodía. Sin embargo, aproximadamente cada 33 años ocurre un equinoccio vernal muy cerca de la medianoche, entre esos dos pares y forma un período quinquenal. Más explícitamente, esta situación ocurre predominantemente cada 33 años y, a veces, con mucha menos frecuencia, después de un intervalo de 29 años.

El primer año bisiesto del ciclo de 33 años es quinquenal y los otros siete cuatrienales. Por lo tanto, las intercalaciones se aplican a los años: 5, 9, 13, 17, 21, 25, 29, 33. El ciclo total asciende a 25 x 365 + 8 x 366 = 12.053 días calendario. En comparación, la duración del tiempo solar es actualmente de 33 x 365,242362 = 12052,99795 días. Esto significa que un ciclo de 33 años se adelanta en 0,00205 días, o aproximadamente 3 minutos, con respecto al tiempo solar. Esta Es la razón por la cual un ciclo estricto de 33 años necesita ajustes futuros. Suponiendo una duración constante para el año equinoccio-vernal, después de aproximadamente 500 ciclos, o aproximadamente 16.000 años, el avance sumaría hasta 1 día. Sin embargo, dado que la duración del año disminuye después de la época +3000 y alcanzaría un valor de aproximadamente 365,24182 días en la época +8000, se requiere un período más corto para que el avance alcance un día completo. De todos modos, cuando el error totaliza 1/33 de un día, el ciclo de 33 años debe acortarse a 29 años para mantener el calendario al ritmo del tiempo solar. Debe enfatizarse que las extrapolaciones detalladas durante períodos muy largos no son válidas porque la duración del año no es constante y, además, perturbaciones desconocidas pueden acumularse en un futuro lejano alcanzando un efecto considerable.

En el pasado, cuando Newton aún no había presentado su teoría de la gravitación y Laplace, Lagrange, Euler, Hamilton y otros no habían contribuido a la formulación de la mecánica celeste, el instante preciso del equinoccio vernal se predijo extrapolando observaciones detalladas. Hoy, gracias a mejoras notables en los modelos de cuerpos orbitales, y más particularmente al desarrollo de computadoras y métodos numéricos potentes, el instante del equinoccio vernal se puede predecir con gran precisión. Sin embargo, se necesitan mediciones basadas en la observación para verificar la correspondencia real entre el modelo matemático y la realidad. Las observaciones también son una parte importante de la cultura del calendario Iraní, y sería prudente preservarlas. Además, ahora que la astronomía aficionada ha hecho grandes avances técnicos, más personas pueden participar en la observación del movimiento solar alrededor de Nowruz. Dado que Nowruz se acompaña de varias ceremonias públicas y festividades, la observación generalizada del Sol alrededor del equinoccio de primavera puede ser un delicioso añadido moderno. Esto también proporcionará una buena oportunidad para enseñarle al público astronomía y las ciencias del calendario. Lo mismo puede recomendarse también para la observación del movimiento solar durante el festival de Mehregân al comienzo de Mehr, el séptimo mes, que celebra el equinoccio de otoño (Notas 15 y 16).

6.- Una observación de interés histórico.

La información sobre la reforma del calendario de Khayyâm no nos llega directamente de él, sino solo a través de breves relatos de astrónomos posteriores. De hecho, 13 años después de la instauración de la reforma, Khayyâm cayó en desgracia después de la muerte de Malek Shah y el asesinato de Nezâm-ol-Molk por Los Asesinos, una orden político-religiosa dirigida por Hasan Sabbâh. Tras la muerte del rey, su esposa gobernó como regente durante dos años, y Khayyâm fue heredero de parte de la hostilidad que ella había demostrado hacia su patrón, Nezâm-ol-Molk, con quien había discutido sobre la cuestión de la sucesión real. Además, los musulmanes ortodoxos, a quienes no les gustaba Khayyâm debido a su libre pensamiento, evidente en sus cuartetas, se hicieron muy influyentes en la corte. Posiblemente tampoco estaban contentos con los movimientos manifiestos de Khayyâm para valorar la identidad persa. Se cortó el apoyo financiero al observatorio y sus actividades, entre las que se encontraba la reforma [del calendario], se detuvieron (Youschkevitch y Rosenfeld 1973).

Sin embargo, no hay duda de que Khayyâm y su grupo implementaron el sistema de intercalación basado en años bisiestos cuatrienales y quinquenales. El astrónomo Khâzeni (Nota 6), que probablemente fue miembro del grupo de reforma y más tarde, durante el reinado de Sanjar, el hijo de Malek Shah, autor del Sanjari zij (observaciones y tablas astronómicas), utiliza las intercalaciones cuadrienal/quinquenal, que muy probablemente provenían del trabajo realizado por el grupo de reforma de Khayyâm. Para un período de 220 años en el calendario Jalâli, Khâzeni calcula 53 intercalaciones, 8 quinquenales y 45 cuadrienal (Nota 17). Unos dos siglos después, el eminente astrónomo y matemático Nasireddin Tusi (1201-1274 A.D.), director del observatorio de Marâgha que creó el Ilkhani zij, y es reconocido por haber hecho una crítica exhaustiva de la astronomía Ptolomeica y por haber presentado un nuevo modelo matemático de movimientos planetarios, da una breve pero importante información sobre la reforma de Jalâli. En su Ilkhani zij, afirma claramente que se aplica una intercalación cada 4 años, lo que hace un año de 366 días, y después de 7 u 8 intercalaciones cuatrienales se realiza una intercalación quinquenal basada en la inducción. Por lo tanto, vemos una referencia implícita al esquema de ciclos de 29 o 33 años. Para obtener información sobre los diversos intentos de intercalación a lo largo de los siglos, basados en el diseño cuadrienal/quinquenal, véase Sayyâd (1981) y el reciente trabajo interesante de Abdollâhi (1996), que trata sobre toda la historia del calendario Iraní.

7. El supuesto ciclo de 2.820 años

Recientemente, algunos expertos del calendario Iraní, principalmente el difunto Behruz (1952) y el difunto Birashk (1993), han sugerido la existencia de ciclos hasta ahora desconocidos en el calendario Iraní. En particular, dividen el calendario en ciclos de 2.820 años, divididos en 21 subciclos de 128 años y 1 subciclo de 132 años (2.820 = 21 x 128 + 132). Los subciclos de 128 y 132 años se dividen en períodos de 29, 33 y 37 años (128 = 29 + 3 x 33; 132 = 29 + 2 x 33 + 37). En resumen, el ciclo consta de 2.137 años ordinarios y 683 años bisiestos.

Este esquema contiene varios inconvenientes. Se afirma que el ciclo de 2.820 años representa el intervalo después del cual los equinoccios vernales se repiten en el mismo instante del día. El escrutinio de los datos de efemérides de IMCCE no nos permite defender esta afirmación, que ya ha sido criticada por investigadores del calendario, entre ellos los astrónomos Iraníes Malakpour (2004) y Sayyâd (2000). Además, todo el ciclo de 2.820 años tiene un adelanto de aproximadamente 0,5 días sobre el tiempo solar. Usando la duración actual del año equinoccio-vernal, el ciclo asciende a 2.820 x 365,242362 = 1.029.983,461 días, mientras que el calendario tendrá 2.137 x 365 + 683 x 366 = 1.029.983 días. Para que el ciclo permanezca en sintonía con el tiempo solar, la duración del año debe ser 365,2421986 días o aproximadamente 365,2422 días. Esta cifra, que resulta también de la fracción 683/2.820, parece ser la duración del año tropical moderno, confundida con la duración del año del equinoccio-vernal. Como resultado, el esquema presenta problemas muchas veces durante un período de 2.025 años, por ejemplo, 21 de marzo 1 AD, 21 de marzo 1600 AD y 21 de marzo 2025 AD.

El ciclo de 2.820 años puede estar en el origen de la duración extremadamente precisa del año (365,24219858156 días) atribuido a Khayyâm (ver arriba, Sección 4). En efecto, la fracción 683/2.820 implica un año de 365,2421985815603 días, que se asemeja sorprendentemente al valor atribuido, lo que arroja dudas sobre su autenticidad. Este valor espurio puede provenir del error de que Khayyâm fue el autor del ciclo de 2.820 años. Sin embargo, no existe un registro histórico que relacione ese ciclo con Khayyâm (Sayyâd 2000). La confusión probablemente se deba al hecho de que Behruz (1952) propuso su esquema en forma de tablas que llamó “tablas Khayyâmicas”, dejando la puerta abierta a interpretaciones erróneas.

Por lo tanto, la concepción de dicho ciclo parece ser el resultado de una confusión entre los años equinoccio-vernales y los años tropicales, como se explicó anteriormente, y además no tiene en cuenta la variación secular de la duración del año. Además, este complejo sistema no hace que el calendario sea más preciso, ya que el esquema de 33 años seguido actualmente, aunque mucho más simple, es muy eficiente.

8. Correspondencia con otros calendarios.

Existen varios códigos de software confiables para convertir las fechas del calendario Iraní y los días de la semana en otros sistemas de calendario y viceversa. Podemos mencionar el “Khayam” Program:

http://payvand.com/calendar

creado por Hossein Bâgher-Zâdeh para la correspondencia entre los calendarios Iraní y Gregoriano. Actualmente, los años bisiestos en los ciclos de 33 años son aquellos años que después de dividir entre 33 dejan un resto de 1, 5, 9, 13, 17, 22, 26 y 30. Por ejemplo, el año AP 1375 que comenzó el 20 de marzo de 1996 tiene un resto de 22 y, por lo tanto, es el año bisiesto. Estas reglas están recogidas en el “programa Khayyam”. En un artículo reciente, Borkowski (1996/1997) argumenta que el algoritmo empleado en ese programa es válido para los años 1799 a 2256 AD. (AP 1178 a 1634). Además, presenta un código conciso que reconstruye el patrón de los años bisiestos en un lapso de tiempo de aproximadamente 3.000 años.

Otra herramienta interesante es el paquete de software Calendrica 2.0, basado en los algoritmos de Calendrical Calculations: The millennium Edition, de Edward M. Reingold y Nachum Dershowitz. La versión on-line:

http://emr.cs.iit.edu/home/reingold/calendar-book/Calendrica.html

permite la conversión no solo entre los sistemas Iraní y Gregoriano, sino también entre varios otros calendarios, principalmente: Armenio, Chino, Francés de la Revolución (Nota 18), Hebreo, Hindú, Islámico, Maya y la versión aritmética errónea del calendario Iraní programado con el ciclo de intercalaciones de 2.820 años.

9. Observaciones sobre el antiguo origen del calendario Iraní.

Los primeros estados Iraníes fueron fundados por los Medos (728-550 a. C.) y los Aqueménidas (550-330 a. C.). Tenemos una cierta cantidad de información sobre los calendarios utilizados durante el período Aqueménida, pero los documentos relacionados con la historia pre-Aqueménida de Irán no solo son escasos sino también silenciosos acerca del calendario durante ese período.

Varias pistas históricas y arqueológicas apuntan a un calendario administrativo lunisolar durante la era Aqueménida, probablemente tomados prestados de los Babilonios. Al mismo tiempo, había un calendario solar ampliamente utilizado por los Iraníes. La razón para adoptar el calendario Babilónico fue ciertamente política. Los Aqueménidas (¿el propio Ciro el Grande?) querían usar el sistema administrativo Babilónico, ya que tenían más experiencia que los Persas. La adopción de este calendario también fue una señal de respeto hacia uno de los pueblos que conformaban el imperio Aqueménida. Del mismo modo, Ciro el Grande rindió respeto oficial a Marduk, el dios supremo de Babilonia durante su ceremonia de coronación. Abdollâhi (1996) da varios argumentos convincentes en apoyo de la influencia Babilónica, mientras que refuta firmemente la opinión de varios trabajadores de que el calendario estatal Aqueménida seguía un modelo egipcio.

Briant, un especialista de la era Aqueménida, refiriéndose a autores antiguos (Plutarco, Diodoro, Quinto Curtio, Dicearchus), cree que existía un calendario solar de 360 días y 5 días epagomenales [NT “los cinco días intercalados del calendario de los Egipcios”], junto con el calendario lunar estatal de tipo Babilónico. Otro hecho histórico corrobora la existencia de un antiguo calendario solar entre los Iraníes durante ese período. Sabemos con certeza que el calendario solar Zoroástrico fue adoptado por los Capadocios después de la conquista de Asia Menor por Ciro el Grande, quien entró en Sardes en 546 a. C. El calendario solar de Capadocia, con 12 meses de 360 días más 5 días epagomenales, era una imitación del calendario Zoroástrico, ya que los nombres de los meses Iraníes y su orden lo hacen especialmente evidente (Enciclopedia Iranica). No olvidemos que después de que Asia Menor quedó bajo el dominio Persa, muchos Iraníes se establecieron en esa región donde, entre otras cosas, establecieron templos de fuego Zoroástricos. Observamos también que en el siglo IV A.D., es decir, unos 700 años después de la conquista de Alejandro, muchas aldeas de Capadocia estuvieron habitadas por los descendientes Iraníes de los primeros colones. El hecho de que durante la dominación Aqueménida los capadocios tomaran prestado el calendario Zoroástrico y no el calendario oficial del estado, señala las profundas raíces de este calendario entre los Iraníes, en particular en lo que respecta a los asuntos culturales y religiosos cotidianos. Y esto implica que el calendario Zoroástrico era más antiguo que la adopción oficial.

Los documentos históricos sobre el calendario Iraní en la antigüedad son tan pocos que no se debe pasar por alto ninguna información. Las explicaciones proporcionadas por Biruni son de suma importancia (de Bloy 1996). En efecto, Biruni ha proporcionado algunas informaciones sobre el calendario preislámico Iraní, que han demostrado ser exactas (Abdollâhi 1996). Biruni, en su Athar al-baqia, nos cuenta sobre el calendario utilizado por los Pishdadis, la dinastía Iraní más antigua según la historia tradicional. Su primer rey fue el mítco Kiumars. A los Pishdadis les sucedieron los Kiyanis, cuyo último rey Dârâ (Darius III) fue asesinado durante la conquista de Irán por parte de Alejandro. Puesto que Biruni cuenta igualmente a Kourosh (Cyrus) y Ardashir (Artaxerxes I Longimanus) entre los Kiyanis, e identifica a los Kianis con los Aqueménidas, los Pishdadis son más antiguos que los Aqueménidas. Y según las leyendas, Nowruz fue establecido por el rey Pishdadi Jamshid (Yima/Yama en la tradición Indo-Iraní), cuyo tiempo se remonta al comienzo del proceso de asentamiento Indo-Iraní y la transición de la caza a la cría de animales, una época muy antigua en que aparentemente ocurrió una glaciación. De todos modos, estas leyendas subrayan la gran antigüedad de Nowruz, así como su importancia cultural.

Según Biruni, los Pishdadis contaban 360 días en un año y 30 días en un mes. Incluían un mes bisiesto cada 6 años y lo llamaban año bisiesto. Luego, cada 120 años, incluían dos meses bisiestos, uno por los 5 días no contados y el otro por los cuartos de día pasados por alto. La duración del año en ese calendario se puede calcular de la siguiente manera (Abdollâhi 1996):

1 año = 12 x 30 = 360 días

6 años = 6 x 360 + 30 = 2.190 días,

120 años = 20 x 2.190 + 30 = 43.830 días, 43.830/120 = 365,25 días,

esto es, 365 días y un cuarto del día. Obviamente, esto es solo posible en un calendario solar. Por lo tanto, si creemos a Biruni, los Iraníes pre-Aqueménidas usaron un calendario solar. Además, las especificaciones anteriores apuntan a un calendario Zoroástrico. Esto implica que, contrariamente a un prejuicio, los Egipcios no fueron los únicos entre las civilizaciones antiguas en usar un calendario solar. No sabemos cuándo comenzó ese calendario, incluso si, según Biruni, el propio Zoroastro introdujo la intercalación mensual. Aunque no sabemos exactamente cuándo vivió Zoroastro (ciertas fuentes Griegas lo ubican en el 6000 B.C., mientras que la tradición lo asocia con el 600 B.C.), estudios recientes sobre las particularidades lingüísticas de los Gathas (la parte más antigua del Avesta, atribuida al propio Zoroastro) sugieren alrededor del 1500 B.C. como su época (Enciclopedia Iranica).

En algún momento se reformó el calendario Iraní: en lugar de practicar una intercalación de un mes completo cada 6 años, los 5 días que faltaban, llamados andargâh, se insertaron después del día 360. La fecha en que se creó el sistema de 365 días es un tema de debate. W.E. West propuso 505 B.C., Markwart lo puso en 493-90, Boyce sugirió inicialmente el período Sasánida, pero recientemente ha revisado su estimación inicial a la era Aqueménida (Enciclopedia Iranica). Pero la cuestión sigue abierta.

La característica sobresaliente del calendario Iraní es Nowruz, que en la creencia Zoroástrica está asociada con el fuego, la séptima creación de Ahura Mazda. Nowruz es, de hecho, el festival más importante del calendario solar Zoroástrico. Según Boyce (op cit. bajo Gâhanbârs), entre los siete antiquísimos festivales Zoroástricos, “solo Nowruz parece tener una justificación doctrinal real, ya que el “nuevo día” se celebraba en el equinoccio de primavera, cuando el Sol, el representante más poderoso de la creación del fuego, está dando calor y vida renovados al mundo … Parece muy probable que Nowruz, con su profundo significado teológico simbólico, fuera establecido por el propio Zoroastro”.

10. Conclusiones

En este artículo, presentamos una descripción detallada del calendario Iraní haciendo hincapié en los fenómenos astronómicos subyacentes, sin ignorar los temas históricos relacionados. Una característica destacada del año Iraní es su punto de partida, Nowruz, que coincide con un evento astronómico: la llegada del Sol al equinoccio vernal. Nowruz, que simboliza el renacimiento de la naturaleza y el triunfo de la vida sobre el opresivo frío y la oscuridad del invierno, es celebrado por un gran número de personas en Asia Occidental y Central.

Sobre la base de las efemérides proporcionadas por el IMCCE francés para el período -4000 a +2500 AD, y las ecuaciones obtenidas por Bretagnon & Rocher (2001) y Meeus (2002), hemos discutido las diversas definiciones del año y demostrado que El calendario Iraní se basa en el año equinoccio-vernal y no en el año “tropical”.

De hecho, el concepto moderno del año “tropical”, formulado por investigadores en el campo de la mecánica celeste, representa un año medio que no depende de un punto de partida particular en la eclíptica. Además, deja de lado las fluctuaciones a corto plazo en la duración del año.

Por lo tanto, el año “tropical” de 365,2422 días no corresponde en absoluto al intervalo entre dos pasos sucesivos del Sol a través del equinoccio vernal. Atribuir el valor de 365,2422 días a dicho intervalo de tiempo es un error, por desgracia ampliamente propagado.

En contraste, el año Iraní, o equinoccio-vernal real, se basa en el movimiento Kepleriano no uniforme de la Tierra alrededor del Sol, así como en las perturbaciones a corto plazo. Es por eso que son necesarias observaciones sucesivas del paso del Sol a través del equinoccio vernal para determinar el instante de inicio del nuevo año y la duración real del anterior.

Sin tener en cuenta las fluctuaciones a corto plazo, la duración media del año Iraní, o equinoccio-vernal, en la época actual es de 365,2424 días solares. Este tiempo representa el intervalo medio entre dos pasos sucesivos del Sol a través del equinoccio vernal.

Sin embargo, la diferencia entre los años “tropical” y equinoccio-vernal no se limita a su duración, ya que sus variaciones a largo plazo también son diferentes.

La confusión entre ambos conceptos no solo es científicamente errónea, sino que puede conllevar otros errores y también puede socavar la precisión del calendario Iraní. Sin embargo, dado que la importancia de este tema a menudo no es tenida en cuenta incluso por los expertos en calendario y los astrónomos, para evitar el error, proponemos usar dos términos distintivos, “año tropical” para el concepto recién introducido y “año equinoccio-vernal” en lo que concierne a los calendarios solares, Iraníes o Gregorianos.

La duración del año, según lo establecido por el sistema de intercalación adoptado por la reforma de Khayyâm, es 365,2424… días. Esta estimación concuerda bien con el año real del equinoccio vernal en la época de Khayyâm, que tenía un valor medio de 365,2423 días, e incluso está más de acuerdo con la duración actual del año del equinoccio vernal, cuyo valor medio es 365,2424 días.

También analizamos el sistema de intercalación incomparable del calendario Iraní, que se basa en un ciclo de 33 años, y señalamos los fundamentos astronómicos de este ciclo. Hay dos tipos de años bisiestos en el calendario Iraní, quinquenal y cuadrienal. El ciclo contiene 8 años bisiestos, el primero quinquenal y los otros siete cuatrienales.

Finalmente, explicamos por qué el ciclo de 2.820 años propuesto recientemente es falaz y argumentamos que lo más probable es que se deba a una confusión entre el año equinoccio-vernal y el año “tropical”. Este ciclo no solo es erróneo, sino que además un esquema de intercalación tan complejo parece inútil para el calendario Iraní, ya que el ciclo de 33 años es casi perfecto. También argumentamos que este esquema está en el origen de la duración extremadamente precisa del año solar atribuido a Khayyâm.

Agradecimientos.

Es un placer agradecer al Institut de Mécanique Céleste et de Calcul des Ephémérides francés (IMCCE), al Dr. Dr. William Thuillot y al Dr. Patrick Rocher por proporcionar las efemérides que fueron esenciales para este estudio y también por sus útiles discusiones. Dado que mi campo de investigación en astrofísica está muy alejado del de los calendarios y el cálculo del tiempo, he aprendido mucho en el proceso de escritura de este documento y me gustaría agradecer a todas las personas que han participado en este proyecto. Estoy particularmente en deuda con el experto en calendarios, Simon Cassidy, Emeryville, California. EE. UU., Por numerosos intercambios de correo electrónico y por una lectura crítica del documento que contribuyó a mejorar su contenido. Le expreso mi profunda gratitud. También me beneficié de las discusiones y comentarios de varios colegas del Observatorio de París, en particular el Dr. Thibaut Le Bertre, el Dr. Jean-François Lestrade y el Dr. James Lequeux. Me gustaría expresarles mi agradecimiento. También estoy agradecido al Dr. Vassilis Charmandaris, Universidad de Cornell, EE. UU., por sus comentarios. También agradezco al Sr. Frédéric Meynadier, Observatorio de París/Universidad Paris VI, por su valiosa y eficiente cooperación. También estoy agradecido al Sr. Jean Meeus, Bruselas, y al Dr. Iraj Malakpour, Instituto de Geofísica, Teherán, por responder a mis preguntas. También quisiera agradecer a los Dres. Edward M. Reingold y Nachum Dershowitz, así como el Dr. Hossein Bâgher-Zâdeh, por usar sus códigos de conversión de calendario. También estoy agradecido al Dr. Kazimierz M. Borkowski, del Observatorio de Radioastronomía de Torun, Universidad Nicolaus Copernicus, Polonia, que leyó el documento e hizo varios comentarios interesantes. También quiero agradecer al Dr. Jafar Âghâyâni-Châvoshi, Sharif University, Teherán, por proporcionar varios documentos históricos. También estoy agradecido al Dr. M.-Sch. Adib-Soltâni, Teherán, por sus comentarios, en particular sobre la etimología. Finalmente, me gustaría dedicar este artículo a la memoria de los difuntos eruditos Zabih Behruz y Ahmad Birashk, quienes iniciaron la investigación moderna sobre el calendario Iraní.

Notas

Según el calendario gregoriano. Corresponde al 15 de marzo en el calendario juliano.

Etimología de Nowruz. En persa moderno now “nuevo”, nôk en persa medio, nava- en Avéstico, nava- en Sánscrito, similar al neos Griego, al novus latino, todos de la raíz indoeuropea *newos. El new inglés, neu Alemán y nouveau, neuf Francés pertenecen a este grupo. El segundo componente, ruz “día” en Persa Moderno, rôc en Persa Medio, raucah en Persa Antiguo, raocah- Avéstico “luz, luminoso; luz diurna”, roka- Sánscrito “brillo, luz”, afín al leukos Griego “blanco, claro”, lux Latino “luz” (también lumen, luna), raíz indoeuropea *leuk- “luz, brillo”. Las palabras Persas rowshan “brillante, claro”, foruq “luz” y afruxtan “iluminar, encender” también pertenecen a esta familia, así como el Inglés light, el Alemán Licht y la lumière Francesa.

No hay ambigüedad entre los equinoccios vernales y otoñales, ¡incluso aunque el paso del Sol a través del equinoccio otoñal es el comienzo de la primavera en el hemisferio sur! El equinoccio vernal es el punto con coordenadas 0,0 grados en el sistema eclíptico, mientras que el equinoccio de otoño se define por el punto 180,0 grados.

Colocar el comienzo del día a medianoche es una práctica Iraní antigua, como lo atestiguan varias fuentes. Por ejemplo, el famoso científico Abu-Rayhân Biruni (A.D. 973-1048) trata este asunto en su conocido libro Athar al-Baqia (historia antigua y geografía), escrito alrededor del año 1000 A.D. (ver más abajo, referencias, para más detalles). ) Además, subraya que el Shahriyâr zij, los cálculos astronómicos y las tablas establecidas durante el reinado del emperador Sasánida Khosrow I Anushiravân alrededor del año 555 A.D., se basaron en la adopción de la medianoche como el comienzo del día. Téngase en cuenta la adopción de la medianoche para el comienzo del día por los astrónomos es relativamente reciente en el mundo occidental. De hecho, hasta 1925, los astrónomos comenzaron y terminaron sus días al mediodía, por lo que el día en el sistema Greenwich Mean Time (GMT) originalmente comenzaba y terminaba al mediodía solar en Greenwich, mientras que en el Greenwich Civil Time comenzaba a medianoche. Sin embargo, los días julianos, utilizados por los astrónomos, comienzan al mediodía (GMT).

De conformidad con el calendario gregoriano. Corresponde al 19 de marzo en el calendario juliano. Taqizâdeh da el 17 de marzo de 622 A.D., lo cual es erróneo, como señaló el primero Birashk.

Según diversas fuentes, hasta ocho astrónomos participaron en el proyecto de reforma. Además de Omar Khayyâm, los otros nombres registrados son: Abu-Hâtam Mozaffar Esfazâri, Abd-ol-Rahmân Khâzeni, Meymun ebn-e Najib Vâseti y Abol-Abbas Lukari. Algunos historiadores han cuestionado la participación de Khâzeni, un niño esclavo de origen bizantino, propiedad de Ali ebn-e Khâzen Marwazi, tesorero y canciller de la corte en Marv (ahora Mary, Turkmenistán), quien le dio al joven la mejor educación posible en disciplinas matemáticas y filosóficas, de manera que se convirtió en un reconocido matemático/astrónomo y “físico”. Khâzeni estableció un zij para el gobernante Sanjar e inventó una balanza para medir pesos específicos que eran tan precisos como los obtenidos ya en el siglo XVIII o principios del siglo XIX. Falleció en 1115 o 1130 d. C., lo que no es incompatible con su participación en la reforma del calendario. Sin embargo, el sistema de intercalación que propone en el Sanjari zij no está totalmente de acuerdo con el esquema de Khayyâm (véase también la Nota 17), y esto puede interpretarse como su no adhesión a la reforma del calendario.

Las actuales duraciones de las estaciones astronómicas, en torno al año 2000, son aproximadamente: primavera 92,76 días, verano 93,65 días, otoño 89,84 días e invierno 88,99 días. Las estaciones son desiguales porque la órbita de la Tierra es ligeramente elíptica y el Sol no está exactamente en el centro de la órbita. Según la segunda ley de Kepler, la Tierra se mueve más rápido cuando está cerca del Sol que cuando está más alejada, por lo que las estaciones que ocurren cuando la Tierra está cerca del Sol pasan más rápido. La Tierra alcanza su perihelio, el punto en su órbita más cercano al Sol, a principios de enero y está en el afelio, más alejado del Sol, a principios de julio. Por lo tanto, el verano es más largo que el invierno en el hemisferio norte. En el hemisferio sur, el invierno es más largo que el verano.

Sin embargo, la situación actual no es eterna y la duración de las estaciones cambia a través del tiempo debido a variaciones en los parámetros orbitales de la Tierra. La precesión, el movimiento de la orientación del eje de rotación de la Tierra, cambia las posiciones de los solsticios y equinoccios con respecto al perihelio. Se necesitan unos 21,000 años (precesión climática) para que estos puntos hagan un circuito completo a lo largo de la órbita, con respecto al perihelio. De manera similar, las variaciones en la forma, o la excentricidad, de la órbita de la Tierra (Nota 14), que tienen una periodicidad de aproximadamente 100.000 años, modifican la duración de las estaciones. Y finalmente, los cambios en la oblicuidad, o inclinación, del eje de la Tierra causan variaciones importantes en la cantidad de radiación solar recibida por la Tierra en latitudes altas, provocando alteraciones considerables en el clima estacional. La oblicuidad, que actualmente es de aproximadamente 23,5 grados, varía entre aproximadamente 22,5 y 24,5 grados en un período de aproximadamente 41.000 años.

El Avéstico, el idioma del Avesta, escrituras del Zoroastrismo, pertenece al grupo Iraní de la familia de lenguas Indoeuropeas. La parte más antigua del Avesta, llamada Gathas (himnos, canciones), compuesta de poemas atribuidos al propio Zaratustra, ahora se cree que datan de alrededor del final del segundo milenio BC y, por lo tanto, son contemporáneos del Sánscrito Védico.

Una breve nota etimológica. “Tropical” de “trópico”, de L.L. tropicus “o perteneciente al solsticio”, de L. tropicus “relativo a un giro”, del Griego tropikos “o relativo a un giro o cambio, o al solsticio” (como sustantivo, “el solsticio”), de tropos “giro, camino, manera, estilo”, tropein “girar”. Raíz indoeuropea *trep- “girar”. Otros términos del mismo origen en inglés: troubadour, trover, contrive, retrieve, trophy, entropy [trovador, descubridor, inventar, recuperar, trofeo, entropía].

La relación entre las nociones de “trópico” y “solsticio” se debe al hecho observable de que el Sol aparentemente “retrocede” después de alcanzar su punto más septentrional (o meridional) en el cielo donde parece detenerse (solsticio, del L. solstitium, de sol “Sol” + -stit-, stes “de pie”, similar a stare “pararse”, en Griego histanai “hacer pararse”, Sánscrito sthâ- “pararse”, Avéstico stâ- “pararse” , Persa istâdan “pararse”, raíz Indoeuropea: *stâ- “pararse”).

El término “trópico” se atestigua alrededor de 1350-1400 en Inglés con el significado de “cualquiera de los dos círculos en la esfera celeste que describen los puntos más septentrionales y meridionales de la eclíptica”. Ampliado en 1527 a los paralelos de latitud correspondientes en el globo terrestre, uno (trópico de Cáncer) 23° 27′ norte, y el otro (trópico de Capricornio) 23° 27′ sur del ecuador, siendo los límites de la zona tórrida. El significado de “región entre estos paralelos” data de 1837. “Tropical” se utilizó por primera vez en 1520-1530, y “año tropical” se atestigua por primera vez en 1585-1595.

Para una descripción interesante de la historia del año tropical, ver Meeus y Savoie (1992).

Por ejemplo, el sitio web del Royal Greenwich Observatory / National Maritime Museum website [https://www.rmg.co.uk/national-maritime-museum], afirma que: “El año se define como el intervalo entre dos pasos sucesivos del Sol a través del equinoccio vernal. Por supuesto, lo que realmente está ocurriendo es que la Tierra está girando alrededor del Sol, pero es más fácil entender lo que está sucediendo considerando el movimiento aparente del Sol en el cielo. El equinoccio vernal es el instante en que el Sol se sitúa por encima del ecuador de la Tierra mientras va del sur al norte. Es el momento que los astrónomos toman como definición del comienzo de la primavera. El año tal como se acaba de definir se llama año tropical y es la duración del año la que marca la repetición de las estaciones. La duración del año tropical es 365,24219 días “. Notamos la confusión ampliamente extendida entre los años tropical y equinoccio-vernal, lo que lleva a un valor erróneo dado para el intervalo medio entre dos pasos sucesivos del Sol a través del equinoccio vernal. El valor correcto es 365.2424 días.

Otros ejemplos del mismo error: “Año Tropical: el año definido por dos pasos sucesivos del Sol a través del equinoccio vernal: 365,242191 días” (Dictionary of Science and Technology, 1992, Academic Press, Inc.). “Año Tropical: el intervalo de tiempo entre dos pasos sucesivos del Sol a través del equinoccio vernal. Su longitud es 365,2422 días solares medios”. (Encyclopedia of Astronomy and Astrophysics, 2001, Institute of Physics Publishing).

El calendario gregoriano también es comparable al año equinoccio-vernal en el sentido de que el objetivo principal y declarado de la reforma gregoriana era evitar que el instante del equinoccio de primavera se alejara de la fecha del 21 de marzo. Desde el primer Concilio de Nicea en el año 325 A.D., el 21 de marzo se adoptó como la fecha eclesiástica del equinoccio de primavera para celebrar la Pascua: el primer Domingo después de la primera luna llena eclesiástica que ocurre el día del equinoccio de primavera o después. La discusión sobre la precisión con la que el calendario gregoriano logra mantener el equinoccio vernal el 21 de marzo está fuera del alcance de esta nota.

El parámetro Delta-T, que solo puede deducirse de las observaciones, depende en gran medida de la velocidad de rotación de la Tierra, que es incierta a nivel de milisegundos. La expresión Delta-T utilizada en la presente efemérides IMCCE es:

Delta-T = 102.3 + 123.5 T + 32.5 T ² segundos

(Morrison y Stephenson 1982), donde T se mide en siglos desde la época J2000.0. Utilizando una muestra más grande de observaciones de los eclipses históricos solares y lunares, Stephenson y Houlden (1986) obtienen una expresión más precisa para el parámetro Delta-T perteneciente a las épocas anteriores al año 948 A.D.:

Delta-T = 2.715,6 + 573,36 T + 46,5 T segundos.

Además, según una revisión reciente de Stephenson (2002), la velocidad de rotación terrestre no está disminuyendo continuamente, sino que sufre variaciones con un ciclo de aproximadamente 1500 años por el cual ahora estamos en un período de siglos sin desaceleración. Aunque las principales causas de los cambios a largo plazo en la duración del día son las mareas lunares y solares que producen un aumento constante en la duración del día de aproximadamente 2,3 milisegundos por siglo, hay un componente significativo no mareal que causa una disminución secular en la duración del día a una tasa media de 0.6 milisegundos por siglo. Por lo tanto, un análisis parabólico simple de Delta-T no es una representación ideal de la realidad. Estas variaciones, si se confirman en investigaciones futuras, no deberían tener un efecto importante en los datos IMCCE promediados presentados en este documento. En cuanto a la duración actual del año (época +2000) medida en días solares reales (Tabla 4, columna 1), la verdad probablemente se encuentra en algún punto entre los valores de día solar y de día uniforme.

Meeus (2002) ha llamado al año equinoccio-vernal año equinoccio-equinoccial. Esto también es engañoso ya que los años vernales y otoñales no son idénticos.

La forma de la órbita de la Tierra alrededor del Sol, descrita por un parámetro llamado excentricidad, cambia periódicamente debido a la atracción gravitacional de los planetas. La excentricidad varía entre 0,070 (elipse alargada) y 0,003 (casi círculo) durante unos 100.000 años. Actualmente la excentricidad es de 0,017, pero se volverá casi circular en unos 25.000 años. Como resultado, la diferencia entre los años tropical y equinoccio-vernal tenderá a cero.

Para más información sobre Mitra o Mehr, quien ha dado su nombre al séptimo mes del calendario Iraní, y también su relación con Navidad y Marianne, el símbolo francés de la república, ver M. Heydari-Malayeri, D’où vient le bonnet de Marianne?

http://wwwusr.obspm.fr/~heydari/divers/marianne.html

Para una discusión sobre el nombre del cuarto mes Iraní, ver: M. Heydari-Malayeri, Tishtar, the Iranian Sirius (en preparación).

El hecho de que el ciclo de 220 años (con un promedio de 365,2409 días) se pueda dividir en ciclos de 29 y 25 años (220 = 5 * 29 + 3 * 25), implicaría que Khâzeni no utilizó el ciclo de 33años (365,2424 días / año). Por lo tanto, si no hay otra información disponible de Khâzeni, uno debería concluir que o bien ha sido copiado erróneamente en los textos que nos han llegado o bien que él malinterpretó o desconfió de Khayyâm.

Según varias indicaciones históricas, el calendario Iraní ha sido una fuente de inspiración para los creadores del calendario revolucionario francés, que preferían un sistema de cálculo del tiempo no religioso, basado en estaciones naturales. De hecho, durante la época de la Ilustración los eruditos europeos se propusieron conocer las culturas y civilizaciones orientales en general. La primera traducción del texto sagrado zoroástrico Avesta a un idioma europeo fue realizada por Abraham Anquetil-Duperron al francés en 1771. También es muy probable que los pensadores revolucionarios franceses conocieran el calendario Iraní a través de varias obras publicadas. Podemos, por ejemplo, mencionar: Freret, De l’ancienne année des Perses, 1742, publicado en l’Histoire de l’Académie Royale des inscriptions et belles lettres, tomo 16, París, 1751 y Gilbert, Nouvelles observations sur l’année des anciens Perses, en l’Histoire de l’Académie Royale des inscriptions, tome 31, Paris, 1788. Para obtener más información, consulte el interesante artículo reciente de Shafâ (2003) que destaca los elementos persas en el calendario revolucionario francés.

Referencias

Abdollâhi, Rezâ, AP 1375 (AD 1996), Târix-e Târix dar Irân (La historia del calendario en Iran), Tehran, Amir Kabir (ie Persa)

Behruz, Zabih, AP 1331 (AD 1952), Taqvim va Târix dar Irân (La medida del tiempo & el calendario en Iran), Tehran, Iran-kudeh, No 15 (in Persian)

Birashk, Ahmad, 1993, A Comparative Calendar of Iranian, Muslim Lunar, and Christian Eras for 3000 Years, Mazda Publishers, Bibliotheca Persica, Costa Mesa, California and New York

Biruni, Abu-Rayhân , 1000, Athar al-Baqia ‘an al-Qurun al-Khalia, tranducido al Inglés como The Chronology of Ancient Nations by Edward C. Sachau, London 1879 (William H. Allen)

de Bloy, François, 1996, The Persian Calendar, J. Brit. Inst. Persian Studies 34, 39

Borkowski, Kazimierz M., 1996/1997, The Persian calendar for 3000 years, Earth, Moon and Planets 74, No 3, 223

Bretagnon, Pierre, Rocher, Patrick, 2001, Du Temps universel au Temps coordonnée barycentrique, Revue du Palais de la Découverte 285, février, p. 39

Briant, Pierre, Histoire de l’Empire Perse, 1996, Fayard, p. 292

Cassidy, Simon, 1996, Error in Statement of Tropical Year

Encyclopedia Iranica, ed. Ehsan Yarshater, Columbia University, Eisenbrauns, , Winona Lake, Indiana

Malakpour, Iraj, 2004, private communication

Meeus, Jean, 2002, More Mathematical Astronomy Morsels, William-Bell Inc., Richmond, Virginia, Ch. 63

Meeus, Jean, Savoie, Denis, 1992, The history of the tropical year, J. Br. Astron. 102, 1

Morrison, L.V., Stephenson, F.R., 1982, Sun and Planetary System 96, 73, Reidel, Dordrecht

O’Connor, John J., Robertson, Edmund F., 1999, The MacTutor History of Mathematics archive, Omar Khayyam

Sayyâd, Mohammad R., 1981 (A.P. 1360), The sequence of quadriennial and quinquennial intercalations in the Jalâli calendar (in Persian), Proceedings of the 12-th Mathematics Conference, Isfahân University, p. 33

Sayyâd, Mohammad R., 2000, Farhang, Quarterly J. of Humanities & Cultural Studies, vol. 12, No. 29-32, Issue topics: Commemoration of Khayyâm, p. 53 (in Persian)

Seidelmann, P. K., Guinot, B., Doggett, L.E., 1992, en Explanatory Supplement to the Astronomical Almanac, University Science Books, Mill Valley, Californian, ed. P. K. Seidelmann, p. 80

Shafâ, Shojâedin (2003), en Persian Heritage, No 30 (tâbestan-e A.P. 1382), p. 39 (in Persian)

Simon, J.L., Bretagnon, P., Chapront, J., Chapront-Touzé, Francou, G., Laskar, J., 1994, & Astrophy. 282, 663

Stephenson, F. Richard, 2003, Historical eclipses and Earth’s rotation, Astronomy & Geophysics 44 (2), 22

Stephenson, F.R., Houlden, M.A., 1986, Atlas of Historical Eclipse Maps, page x, Cambridge University Press

Taqizâdeh, S. H., 1938, Old Iranian Calendars, Royal Asiatic Society

Youschkevitch, A.P., Rosenfeld, B.A., 1973, “al-Khayyami”, Dictionary of Scientific Biography VIII, p. 323

ASTRONOMÍA, CIENCIA, MATEMÁTICAS irania